Next: Applications
Up: Computational Astrophysics
Previous: Identification and Analysis of Binary Star Systems using Probability Theory
Table of Contents -- Index -- PS reprint -- PDF reprint
Astronomical Data Analysis Software and Systems VII
ASP Conference Series, Vol. 145, 1998
Editors: R. Albrecht, R. N. Hook and H. A. Bushouse
Grzegorz Po ubek
ubek
Astronomical Institute of the Wroc aw University
PL-51-622 Wroc
aw University
PL-51-622 Wroc aw, ul. Kopernika 11, Poland
aw, ul. Kopernika 11, Poland
Abstract:
We present a computer program for modelling energy flux
distribution and light curves of eclipsing binaries from far
ultraviolet to infrared regions. The Roche model is assumed.
Proximity effects of components
(reflection of radiation and surface gravity darkening) are taken into
account. The calculations are made in the absolute flux units and
the newest Kurucz's (1996) models of stellar atmospheres are used.
As an example, we consider the Algol (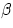 Persei) system, where an
eclipsing pair (Algol A-B) is accompanied by the third
component (Algol C).
Persei) system, where an
eclipsing pair (Algol A-B) is accompanied by the third
component (Algol C).
The photospheres of eclipsing components are represented by a
grid of surface elements, which are treated as
plane-parallel and homogeneous ones.
In order to calculate the synthetic fluxes of radiation an integration
over all surface elements visible at a given orbital
phase, 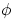 , should be done.
For this purpose geometrical parameters (i.e., area of elements
and their positions) as well as physical ones (temperatures and surface
gravities) for all elements have to be known.
To describe the system's geometry we assumed the Roche model
presented by Kopal (1959) and
Limber (1963) for synchronous and nonsynchronous rotation,
respectively.
, should be done.
For this purpose geometrical parameters (i.e., area of elements
and their positions) as well as physical ones (temperatures and surface
gravities) for all elements have to be known.
To describe the system's geometry we assumed the Roche model
presented by Kopal (1959) and
Limber (1963) for synchronous and nonsynchronous rotation,
respectively.
Figure 1:
The surface temperature distribution for
Algol A-B system before (upper plot) and after (lower
plot) correction for temperature due to the irradiation effect.
It is clearly seen that the irradiation effect affects
mainly the B component's temperature distribution.
The binary system is displayed at orbital phase 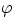 = 0.3.
= 0.3.
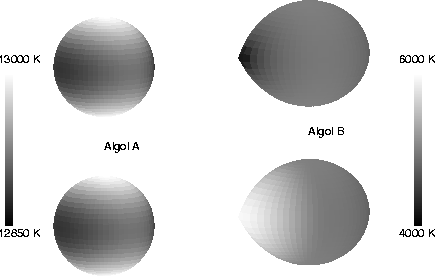 |
Assuming synchronous rotation of the components, the
total potential 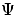 can be written as:
can be written as:
| ![\begin{displaymath}
{\Psi} = G \frac{M_A}{r_1} + G \frac{M_B}{r_2} + \frac{{\omega}^2}{2}
\left[ (x-\frac{a M_B}{M_A + M_B})^2 + y^2 \right],\end{displaymath}](img81.gif) |
(1) |
where MA and MB are stellar masses, a - orbital separation
of components, 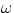 - angular velocity of the system about the
z-axis, G - the gravitational constant,
r12 = x2 + y2 + z2, and r22 = (a-x)2 + y2 + z2.
Using spherical polar coordinates (
- angular velocity of the system about the
z-axis, G - the gravitational constant,
r12 = x2 + y2 + z2, and r22 = (a-x)2 + y2 + z2.
Using spherical polar coordinates (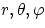 )equation (1) can be rewritten as:
)equation (1) can be rewritten as:
| ![\begin{displaymath}
{\Omega} = \frac{1}{r} + q \left[ \frac{1}{(1-2{l}r + r^2)^\frac{1}{2}}
- {l}r \right] + \frac{1}{2}(1+q)(1-{n}^2) r^2 \, ,\end{displaymath}](img84.gif) |
(2) |
where q=MB/MA, 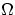 is the dimensionless
Roche potential
is the dimensionless
Roche potential
| 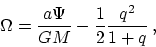 |
(3) |
and l, m, n are direction cosines of the radius vector, i.e.
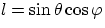 ,
, 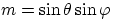 ,and
,and 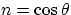 .If we assume that the photospheres of primary and secondary
components are equipotential surfaces
with potentials
.If we assume that the photospheres of primary and secondary
components are equipotential surfaces
with potentials 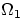 and
and 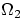 , respectively, then the equation
(2) allows us to determine the total surfaces of both components.
We solve this equation by the iterative Newton-Raphson method.
, respectively, then the equation
(2) allows us to determine the total surfaces of both components.
We solve this equation by the iterative Newton-Raphson method.
The local surface gravity follows from the equation
If we neglect the effect of irradiation by the companion, the
temperature at (i,j)-point of the surface grid depends only on
the local value of gravity
| 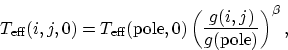 |
(4) |
where 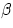 is the gravity-darkening exponent.
Index 0 refers to effective temperatures in case of neglecting
of the irradiation effect (hereafter referred to as intrinsic ones).
For photospheres in radiative equilibrium the integral flux is
proportional to the local value of gravity (von Zeipel 1924)
which implies
is the gravity-darkening exponent.
Index 0 refers to effective temperatures in case of neglecting
of the irradiation effect (hereafter referred to as intrinsic ones).
For photospheres in radiative equilibrium the integral flux is
proportional to the local value of gravity (von Zeipel 1924)
which implies 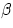 = 0.25.
The gravity-darkening exponent is smaller for photospheres
with convection and in case of thick convective
envelope
= 0.25.
The gravity-darkening exponent is smaller for photospheres
with convection and in case of thick convective
envelope 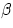 = 0.08 (Lucy 1967).
= 0.08 (Lucy 1967).
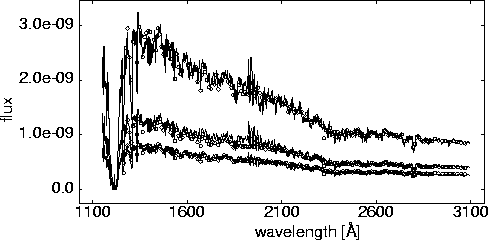
Figure 2:
Examples of IUE spectra of Algol (solid lines)
in 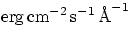 , in
comparison with the best-fit model calculations (circles)
for orbital phases
, in
comparison with the best-fit model calculations (circles)
for orbital phases 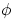 = 0.925, 0.979, 0.996.
= 0.925, 0.979, 0.996.
 |
If we take into account the irradiation effect,
the local temperatures have to be modified.
For this purpose an iterative procedure based on
the Chen & Rhein (1969) approach was used.
In the first step, the intrinsic effective
temperatures of both components were set.
Then, for each surface element
(i,j) of the given component
the flux F(i,j) received from the other component
was evaluated.
The corrected temperature 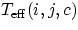 follows from the equation
follows from the equation
| 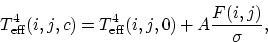 |
(5) |
where A is bolometric albedo, 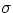 - Stefan-Boltzmann constant.
A was assumed to be constant over the stellar surfaces.
In the case of radiative equilibrium all absorbed energy must
be re-emitted; this means that A equals 1.0.
For the convective models the bolometric albedo
can be smaller than 1.0 and we assume A = 0.5
(cf. Rucinski 1969).
The influence of the irradiation effect for the Algol eclipsing pair
is shown in Figure 1.
Next, we calculate the radiation flux received from the system:
- Stefan-Boltzmann constant.
A was assumed to be constant over the stellar surfaces.
In the case of radiative equilibrium all absorbed energy must
be re-emitted; this means that A equals 1.0.
For the convective models the bolometric albedo
can be smaller than 1.0 and we assume A = 0.5
(cf. Rucinski 1969).
The influence of the irradiation effect for the Algol eclipsing pair
is shown in Figure 1.
Next, we calculate the radiation flux received from the system:
| 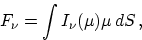 |
(6) |
where integration extends over visible parts of all components,
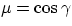 (
(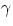 is the
angle between the surface normal and the line of sight).
In this paper we use the second-order limb-darkening law
for the evaluation of the specific intensity
is the
angle between the surface normal and the line of sight).
In this paper we use the second-order limb-darkening law
for the evaluation of the specific intensity
| ![\begin{displaymath}
I_{\nu}(\mu) = I_{\nu}(1) [1 - u_1(1-\mu) - u_2(1-\mu)^2].\end{displaymath}](img101.gif) |
(7) |
The coefficients u1 and u2, defined by
Wade & Rucinski (1985), were calculated for
Kurucz's (1996) unpublished models of stellar atmospheres.
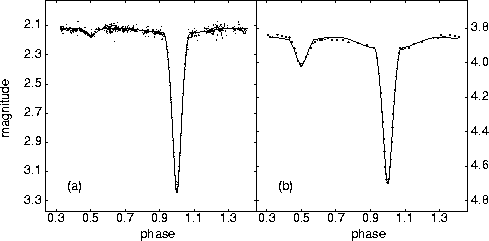
Figure 3:
Comparison of the theoretical light curves of Algol
(solid lines) with observations (dots) in Johnson V band (a)
and in the infrared at 1.6  m (b).
m (b).
 |
We analyse UV spectra of Algol collected by
the IUE satellite.
We use 15 pairs of IUE spectra from short wavelength primary
(SWP) and long wavelength primary (LWP) cameras.
We found 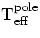 (Algol A) = 13000 K,
(Algol A) = 13000 K,
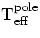 (Algol B) = 5000 K,
(Algol B) = 5000 K,
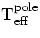 (Algol C) = 7000 K,
(Algol C) = 7000 K,
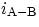 =
= 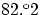 and other parameters similar to those
given by Tomkin & Lambert (1978). The best-fit solution for the
three pairs of spectra is displayed in Figure 2.
This model was further verified by UBV observations of
Algol taken from Wilson et al. (1972) and by the infrared
observations of Chen & Reuning (1966).
The comparison of these observations with the theoretical
light curves are shown in Figure 3.
and other parameters similar to those
given by Tomkin & Lambert (1978). The best-fit solution for the
three pairs of spectra is displayed in Figure 2.
This model was further verified by UBV observations of
Algol taken from Wilson et al. (1972) and by the infrared
observations of Chen & Reuning (1966).
The comparison of these observations with the theoretical
light curves are shown in Figure 3.
Acknowledgments:
This work was supported by the research grant
No. 2 P03D 001 08
from the Polish Scientific Research Committee (KBN).
References:
Chen, K.-Y., & Reuning, E. G., 1966, AJ, 71, 283
Chen, K. -Y., & Rhein, W. J., 1969, PASP, 81, 387
Kopal, Z., 1959, Close Binary Systems, International Astrophysics
Series Vol. 5
Kurucz, R.L., 1996, CD-ROM No.19
Limber, D.N., 1963, ApJ, 138, 1112
Lucy, L.B., 1967, Z. Astrophys., 65, 89
Rucinski, S.M., 1969, Acta Astron., 19, 245
Tomkin, J., & Lambert, D. L., 1978,
ApJ, 222, L119
Wade, R. A., & Rucinski, S. M., 1985, A&AS, 60, 471
Wilson, R. E., DeLuccia, M. R., Johnson, K.,
& Mango, S. A., 1972, ApJ, 177, 191
von Zeipel, H., 1924, MNRAS, 84, 702
© Copyright 1998 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: Applications
Up: Computational Astrophysics
Previous: Identification and Analysis of Binary Star Systems using Probability Theory
Table of Contents -- Index -- PS reprint -- PDF reprint
payne@stsci.edu
![]() ubek
ubek![]() aw University
PL-51-622 Wroc
aw University
PL-51-622 Wroc![]() aw, ul. Kopernika 11, Poland
aw, ul. Kopernika 11, Poland![]() , should be done.
For this purpose geometrical parameters (i.e., area of elements
and their positions) as well as physical ones (temperatures and surface
gravities) for all elements have to be known.
To describe the system's geometry we assumed the Roche model
presented by Kopal (1959) and
Limber (1963) for synchronous and nonsynchronous rotation,
respectively.
, should be done.
For this purpose geometrical parameters (i.e., area of elements
and their positions) as well as physical ones (temperatures and surface
gravities) for all elements have to be known.
To describe the system's geometry we assumed the Roche model
presented by Kopal (1959) and
Limber (1963) for synchronous and nonsynchronous rotation,
respectively.
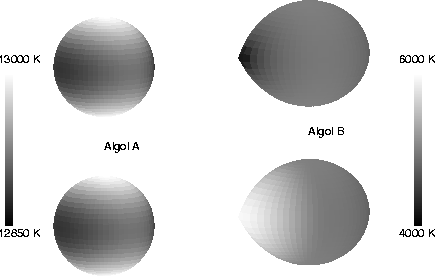
![\begin{displaymath}
{\Omega} = \frac{1}{r} + q \left[ \frac{1}{(1-2{l}r + r^2)^\frac{1}{2}}
- {l}r \right] + \frac{1}{2}(1+q)(1-{n}^2) r^2 \, ,\end{displaymath}](img84.gif)
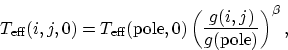


![]() (Algol A) = 13000 K,
(Algol A) = 13000 K,
![]() (Algol B) = 5000 K,
(Algol B) = 5000 K,
![]() (Algol C) = 7000 K,
(Algol C) = 7000 K,
![]() =
= ![]() and other parameters similar to those
given by Tomkin & Lambert (1978). The best-fit solution for the
three pairs of spectra is displayed in Figure 2.
This model was further verified by UBV observations of
Algol taken from Wilson et al. (1972) and by the infrared
observations of Chen & Reuning (1966).
The comparison of these observations with the theoretical
light curves are shown in Figure 3.
and other parameters similar to those
given by Tomkin & Lambert (1978). The best-fit solution for the
three pairs of spectra is displayed in Figure 2.
This model was further verified by UBV observations of
Algol taken from Wilson et al. (1972) and by the infrared
observations of Chen & Reuning (1966).
The comparison of these observations with the theoretical
light curves are shown in Figure 3.