W. Freudling and N. Pirzkal Space Telescope - European Coordinating Facility, Karl-Schwarzschild-Str. 2 , D-85748 Garching, Germany, Emails: wfreudli@eso.org, npirzkal@eso.org
In addition to broad band, medium band and wide band filter sets, the NICMOS Camera 3 (NIC3) filter wheel contains three grisms. These grisms provide low-resolution slitless spectroscopic capabilities. This article describes the wavelength and throughput calibration of the grisms and discusses the photometric performance of the NICMOS grism mode.
NICMOS, Grisms, Calibration
The NICMOS grisms in camera 3 (NIC3) provide low-resolution slitless
spectroscopic capabilities. There are three grisms: G096 covering
0.8 to 1.2 ![]() ;
G141 for 1.1 to 1.9
;
G141 for 1.1 to 1.9 ![]() and G206 for the 1.4 to 2.5
and G206 for the 1.4 to 2.5 ![]() region. The resolution of the first order spectra on all grisms is
about 200 per pixel. Second order spectra contain on the order of 1 to 2%
of the total detected flux for each object on the grism images. In
general, only part of the second order spectra are located on the
detector. Since there are no slits, an image of the same field through
a matching wide-band filter is needed to obtain a zero point for
wavelength calibration. A matching filter with similar throughput as
the grism is available for each of the grisms. A standard procedure
for the grism observations is to spend a small fraction of the total
integration time to obtain the undispersed image.
region. The resolution of the first order spectra on all grisms is
about 200 per pixel. Second order spectra contain on the order of 1 to 2%
of the total detected flux for each object on the grism images. In
general, only part of the second order spectra are located on the
detector. Since there are no slits, an image of the same field through
a matching wide-band filter is needed to obtain a zero point for
wavelength calibration. A matching filter with similar throughput as
the grism is available for each of the grisms. A standard procedure
for the grism observations is to spend a small fraction of the total
integration time to obtain the undispersed image.
The optimum focus position for NIC3 is beyond the reach of the PAM focusing mechanism, i.e. NIC3 can only be perfectly focused by moving the secondary mirror of HST. Since such a move prevents other HST instruments from being focused, it is carried out only during special NIC3 campaigns, the next one is planned for June 1998. The optimum position of the focus has continuously been moved over the last few month to a more favorable location. Wavelength and throughput calibration observations have been carried out both during and outside of NIC3 campaigns.
 |
A detailed description of the methods used to extract spectra from a grism image with a matching direct image is given in Pirzkal & Freudling (1998a, b and c). Here, we briefly summarize the steps relevant for the discussion of the grism calibration given below.
The first step in the extracting is the removal of the background from the location covered by the spectrum. All calibration observations were of sufficient s/n so that the background contribution to the spectrum is small and no differences were found using different background removal procedures.
 |
The flux Fl for a given wavelength bin l is computed
from the background subtracted grism image by summing
the count rates gx,y at pixel position (x,y)
| (10.1) |
For the errors, the error estimate for each pixel is taken from the array 'err' of the input grism image. The error estimate for each wavelength is then the quadratic sum over the same region,
| (10.2) |
The pixels included in the sums are determined by the position of the object on the direct image, and the location of the spectra relative to the direct image. This relative location is parameterized as a shift and a rotation of the spectrum relative to the rows of the image which contains the object on the direct image. These parameters have been determined for each grism and separately for the first and second order.
For the extraction of the calibration spectra, boxcar functions have been used for the weights. For the flux calibration, fairly large apertures have been used to assure that all the flux is contained in the box.
The inverse sensitivity tx,y,l can be written as
![]() ,
where for a given wavelength l, the function qx,y
presents an appropriate normalized monochromatic
flatfield. Unfortunately, narrow-band flatfields for the NIC3 camera
which can be used to approximate monochromatic flatfields are
available only for a very limited number of wavelengths.
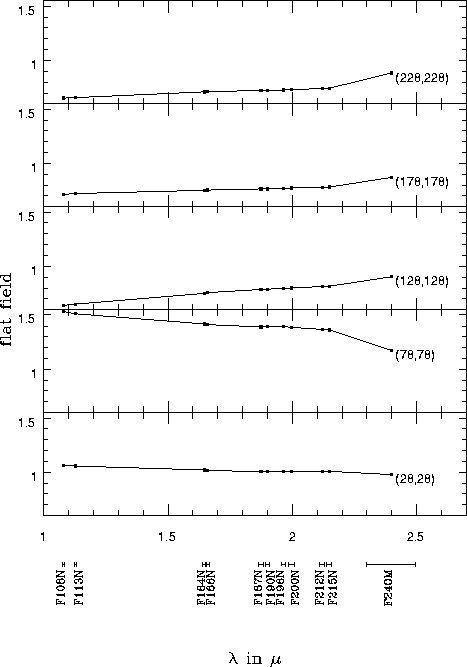
Figure 1 illustrates the situation. The wavelength
dependence of the flatfield response of individual pixels differs
substantially over the detector. Currently, the only way to estimate
the pixel response for a given wavelength is to use this limited data
set and interpolate between the wavelengths of the available filters.
The limited measurements of this response is a major contribution to
our uncertainty in the flux calibration.
,
where for a given wavelength l, the function qx,y
presents an appropriate normalized monochromatic
flatfield. Unfortunately, narrow-band flatfields for the NIC3 camera
which can be used to approximate monochromatic flatfields are
available only for a very limited number of wavelengths.
Figure 1 illustrates the situation. The wavelength
dependence of the flatfield response of individual pixels differs
substantially over the detector. Currently, the only way to estimate
the pixel response for a given wavelength is to use this limited data
set and interpolate between the wavelengths of the available filters.
The limited measurements of this response is a major contribution to
our uncertainty in the flux calibration.
The purpose of the wavelength calibration is to find the relation
between the pixel position relative to the undispersed objects l and
the wavelength
![]() .
The purpose of the flux calibration is to
find the inverse sensitivity
.
The purpose of the flux calibration is to
find the inverse sensitivity
![]() as a function of wavelength
in mJy/DN/sec.
as a function of wavelength
in mJy/DN/sec.
 |
 |
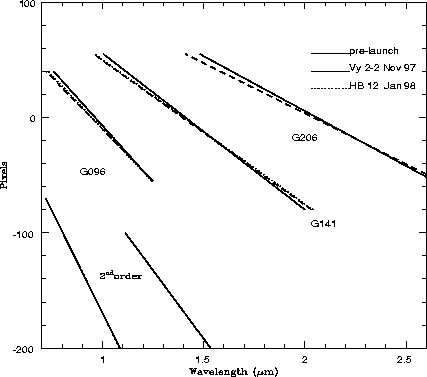
NICMOS has no internal lamps for wavelength calibration. Therefore, objects with strong IR line emission must be used for in-orbit wavelength calibration. For slitless spectroscopy, wavelength calibrators should be compact. The best wavelength calibrators for NICMOS seem to be compact planetary nebulae. The Planetary nebulae Vy 2-2 and HB12 have been used for that purpose. Currently, HB12 is routinely used for monitoring the wavelength dispersion.
The dispersion of the grisms, i.e. the wavelength as a function of
position relative to the coordinate of the object on the direct
images, have been parameterized as linear relations. Polynomials of
higher order have been tried but did not result in better fits. The
parameters of the the dispersion relation were determined by
correlation of the extracted spectra with ground based spectra of Vy
2-2 provided by Hora et al., 1998. The in-orbit measurements of the
dispersion relation are significantly different from the pre-launch
measurements, but no significant changes in the parameters of the
relation have been observed in the repeated in-orbit measurements. As
an illustration, the dispersion relations for 2 epochs are plotted in
figure 2 and compared to the pre-launch measurements. The
main uncertainty in the wavelength calibration is the exact location
of the object on the direct image. The uncertainty for an individual
spectrum is about 0.5 pixels. This translates into an uncertainty of
the wavelength calibration of less than 0.005![]() .
Within this
uncertainty, no dependence of the dispersion relation on the position
on the NICMOS detector. Similarly, no systematic change in time has
been detected so far.
.
Within this
uncertainty, no dependence of the dispersion relation on the position
on the NICMOS detector. Similarly, no systematic change in time has
been detected so far.
The dispersion relations of second order spectra were determined by cross-correlating the extracted spectra of both orders and using the calibration of the first order with the ground-based data.
The white dwarf G191-B2B and the solar analog P330 have been adopted as flux calibrators for NICMOS. Each grism calibration observations consists of at least three different direct image / grism image pairs, with the calibrator positioned at different locations on the NICMOS detector for each individual observation. The first order spectrum from each pair of images was extracted in instrumental units (DN/sec).
For both calibrators, model spectra scaled to measurements at shorter wavelengths are available, for details see Colina (1998, this workshop). The spectra as given by Colina & Bohlin 1997 (for the solar analog P330), and Bohlin & Colina & Finley 1995 and Bohlin 1996 (for the white dwarf G191-B2B) have been used for the grism calibration.
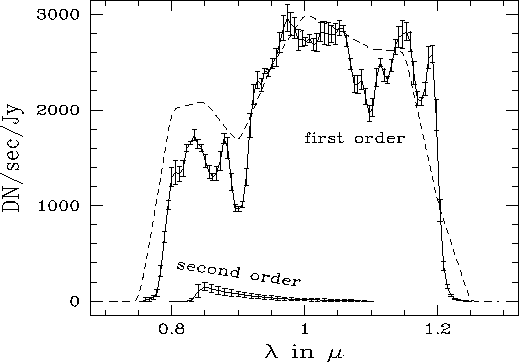
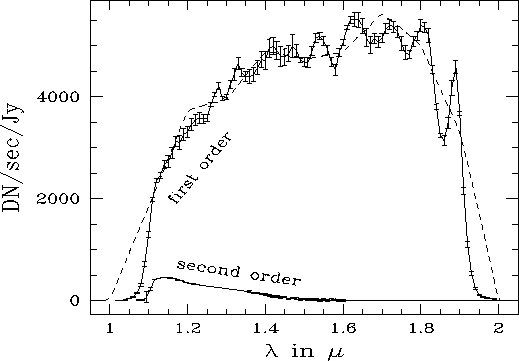
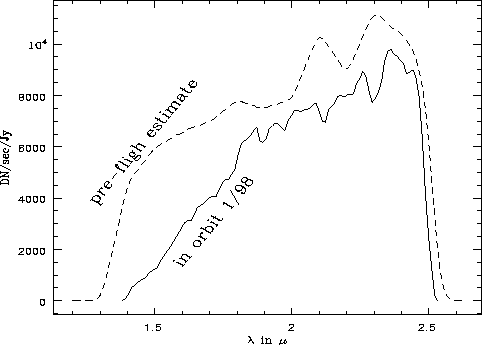
Inverse sensitivity curves for first order spectra were derived by dividing the individual spectra by the model spectrum of the respective calibrator and computing the average of all spectra from the two flux calibrators. Figures 3, 4 and 5 show the derived sensitivities for G096, G141 and G206, respectively. The uncertainty for each point in the sensitivity curves is the rms from all extracted spectra divided by the number of spectra.
Inverse sensitivity curves for second order were derived from archive grism images taken for the public parallel program. Spectra were extracted for bright objects with both first and second order spectra on single grism images. The relative extracted flux for both orders in combination with the first order sensitivity calibration was used to derive the sensitivity of the second order. Since the field of view of grism observations do not allow for both orders to be completely contained in single images, several images had to be used to derive the sensitivity for the whole wavelength range of grisms G098 and G141. The available data did not allow to derive a calibration for the second order of G206.
 |
The sensitivity curves for the first order spectra presented in the previous section have typical uncertainties per point of about 5 to 10%. These errors have been estimated from the differences of individual extracted spectra. We have separated the inverse sensitivity by the calibrator used to derive them and found that integrated over the whole bandpass systematic differences are smaller than 2%. Statistical error as computed from the error array of the grism images are also small compared to the errors shown above. The origin of the uncertainty in the sensitivities are differences in the spectra extracted at different positions on the detector. Presumably, these differences are due to our lack of knowledge of the difference in the wavelength dependence of the individual pixel response. As mentioned in section 2., these differences are currently approximated by the response of narrow-band flats which do not sample the full range of wavelength of the grisms very well. For that reason, the flux calibration of a single spectrum can be up to 20 to 30% uncertain. This is within the goal of the original calibration plan.
We are carrying out wavelength and flux calibrations of the NICMOS
grisms. The uncertainty in the flux calibration is about 5-10% for
the first order spectra, the uncertainty in the wavelength calibration
is less than 0.005![]() .
Files with the most recent calibration data
can be obtained from http://ecf.hq.eso.org/nicmos/. The monitoring of
wavelength and throughput calibration will continue until the end of
1998.
.
Files with the most recent calibration data
can be obtained from http://ecf.hq.eso.org/nicmos/. The monitoring of
wavelength and throughput calibration will continue until the end of
1998.
