Imaging Polarimetry with NICMOS

D. C. Hines¹ Steward Observatory, The University of Arizona, Tucson, AZ 85721

(1)NICMOS Project, The University of Arizona

 

 

Abstract:

The Near Infrared Camera and Multi-Object Spectrometer (NICMOS) contains optics which enable imaging polarimetry at 1 & 2 microns with unprecedented detail. The preflight Thermal Vacuum tests revealed that each polarizer has a unique polarizing efficiency, and that the position angle offsets differ from the nominal positions of 0, 120 & 240. Therefore, to properly reduce polarimetry data obtained with NICMOS, a new algorithm different from that needed for an ideal polarizer was developed. I discuss this new algorithm, its successful application to NICMOS observations, and its more general use for data obtained with other instruments. I also present estimates of the NICMOS Instrumental Polarization, and discuss both the sensitivity of the Grisms to polarized light and the accuracy of NICMOS imaging polarimetry for faint and low polarization objects.

NICMOS, Polarimetry, Data Reduction, IRC +10216, CRL 2688

Introduction

Studies of polarized light have brought about profound changes in our understanding of astronomical objects, especially within the last two decades with the advent of sensitive, large format imaging arrays such as optical CCDs and the NICMOS3 infrared arrays. Imaging of linearly polarized light from young stellar objects, bipolar nebulae, radio galaxies and hyperluminous infrared galaxies has shown that disks of dusty gas play a key role in the birth and death of stars, and can strongly influence the appearance of quasars and QSOs.

The Near Infrared Camera and Multi-Object Spectrometer (NICMOS) contains optical elements which enable high spatial resolution, high sensitivity observations of linearly polarized light from $0.8 - 2.1 \mu$m. The filter wheels for Camera 1 (NIC1) and Camera 2 (NIC2) each contain three polarizing elements sandwiched with band-pass filters. The design specifies that the position angle of the primary axis of each polarizer (as projected onto the detector) be offset by 120 from its neighbor, and that the polarizers have identical efficiencies. While this clean concept was not strictly achieved, the reduction techniques described below permit accurate polarimetry using both the short- and long-wavelength cameras over their full fields of view.

Thermal Vacuum Tests

Preflight thermal vacuum tests on NICMOS included an extensive characterization of the polarimetry optics. We also measured the overall sensitivity of the non-polarimetry optics to polarized light. A polarizing element attached to the CIRCE standard light source provided uniform illumination of the entire field of view with light of known polarization and position angle.

Polarizing efficiencies^12.1 and absolute polarizer position angles (relative to the NICMOS entrance aperture) were derived for each polarizer in NIC1 and NIC2 from images obtained at 20 increments of the calibration polarizer position angle. The same method, but without the NICMOS polarizers in place, was used to to evaluate the polarization signature imparted by the mirrors which comprise the NICMOS imaging system, and to characterize the sensitivity of the NIC3 Grisms to polarized light.

The Thermal Vacuum tests showed that:

• Each polarizer in each camera has a unique polarizing efficiency.

• The offsets between the position angles of the polarizers within each filter wheel differ from their nominal values of 120.

• The instrumental polarization caused by reflections off the mirrors in the NICMOS optical train is small ( $\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}1\%$).

• The Grisms are slightly sensitive to the orientation of incoming polarized light, with G206 showing the largest variation in intensity ($\sim 5\%$) for completely polarized light. This effect scales with percentage polarization and will be negligible for the majority of astronomical situations.

The HSL Algorithm for Reducing NICMOS Polarimetry Observations

The ``standard theory'' polarimetry reduction algorithm outlined in the original NICMOS Manual (Axon et al. 1996) assumes that the polarizers have uniform and perfect (100%) polarizing efficiencies, and that the position angles of the primary axis of the polarizers are offset by exactly 120. The thermal vacuum tests showed that the NICMOS polarizers are not ideal, so a more complex technique is required. The new algorithm developed by Hines, Schmidt & Lytle (1997; hereafter HSL) is presented below.

The observed signal from a polarized source of total intensity I and linear Stokes parameters Q and U measured through the k^th polarizer oriented with a position angle^12.2 $\phi_{k}$ is

$$S_{k} = A_{k}I + \epsilon_{k}(B_{k}Q + C_{k}U),$$ (12.1)

where

$$A_{k} = \frac{1}{2}t_{k}(1+l_{k}),\, B_{k} = A_{k}\cos{2\phi_{k}},\, C_{k} = A_{k}\sin{2\phi_{k}},$$

and $\epsilon_{k}$ is the polarizing efficiency, t_k is the fraction of light transmitted for a 100$\%$ polarized input aligned with the polarizer's axis, and l_k is the fraction transmitted (exclusive of that involved in t_k) when the incoming light is perpendicular to the axis of the polarizer (see Table 1). The values of t_k were initially determined by the filter manufacturer, and were not accurately remeasured in thermal vacuum tests (HSL). However, recent observations of unpolarized and polarized standard stars have allowed us to refine these values.

Table (1) presents the properties of the individual polarizers as determined in preflight thermal vacuum tests and by the on-orbit standard star observations. Table (2) lists the coefficients derived from these parameters for use solving Eq. (1).

 

Table 1: Characteristics of the NICMOS Polarizers

 

Filter	$\phi_{k}$a	$\epsilon_{k}$	tk (on-orbit)b	lk	Comments
POL0S	1.42	0.9717	0.7660	0.0144	...
POL120S	116.30	0.4771	0.5946	0.3540	Possible ``ghost'' images
POL240S	258.72	0.7682	0.7169	0.1311	...
POL0L	8.84	0.7313	0.8981	0.1552	...
POL120L	131.42	0.6288	0.8551	0.2279	...
POL240L	248.18	0.8738	0.9667	0.0673	...

aAs measured from the NICMOS aperture 224.52 about the +U3 axis.

bDerived from on-orbit observations of the unpolarized standard BD 32 3739 (Schmidt, Elston & Lupie 1992).

 

Table: Coefficients for Simultaneous Solution of Equation (1)a

 

Filter	Ak	$\epsilon_{k}$Bk	$\epsilon_{k}$Ck
POL0S	+0.3936	+0.3820	+0.0189
POL120S	+0.4025	-0.1166	-0.1526
POL240S	+0.4054	-0.2876	+0.1195
POL0L	+0.5187	+0.3614	+0.1152
POL120L	+0.5250	-0.0411	-0.3276
POL240L	+0.5159	-0.3262	+0.3111

aBased on thermal vacuum data and the on-orbit determination of t_k (Table 1).

After solving the system of equations (Eq. 1) to derive the Stokes parameters at each pixel (I, Q, U), the percentage polarization (p) and position angle ($\theta$) at that pixel are calculated in the standard way:

$$p = 100\% \times\frac{\sqrt{Q^{2}+U^{2}}}{I}, \theta = \frac{1}{2}{\rm tan}^{-1}\left( \frac{U}{Q} \right).$$

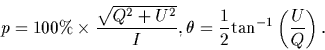
[Note that the arc-tangent function is implemented differently on different systems and programming environments, so care must be taken to ensure that the derived angles place the electric vector in the correct quadrant.]

On-Orbit Calibration

Observations of a polarized star (CHA-DC-F7: Whittet et al. 1992) and an unpolarized (null) standard (BD 32 3739: Schmidt et al. 1992) were obtained with NIC1 and NIC2 (Cycle 7 CAL 7692, 7958: Axon). The observations used a four position, ``spiral-dither'' pattern with 20.5 pixel offsets to improve sampling and alleviate the effects of bad pixels, cosmic rays, some persistence, and other image artifacts. Two epochs were chosen such that the differential telescope roll between observations was $\sim 135\deg$.

Since the thermal vacuum tests showed that the imaging system had little effect on the observed polarization, any measured polarization in the null standard was attributed the t_k term in the HSL algorithm. Applying our refined coefficients to the polarized star data yielded a measured percentage polarization within 0.3$\%$ of the published value. Table 3 presents the results.

 

Table 3: Polarization Measurements of CHA-DC-F7

 

Band	p	$\sigma_{p}$a	$\theta$	$\sigma_{\theta}$a
	$(\%)$	$(\%)$	($\deg$)	($\deg$)
J (ground)b	3.19	0.05	118	2
1$\mu$m (Epoch 1)	3.44	0.5	111	4
1$\mu$m (Epoch 2)	3.31	0.5	108	4
K (ground)b	1.19	0.01	126	4
2$\mu$m (Epoch 1)	0.97	0.2	119	6
2$\mu$m (Epoch 2)	1.00	0.2	119	6

a Conservative upper limits for the uncertainties were estimated from the variation between results obtained from individual ``dither'' positions in each epoch.

bWhittet et al. (1992)

On-Orbit Results

Polarimetry data were obtained for IRC +10216 and CRL 2688 with NIC1 and NIC2 respectively as part of the Early Release Observations program. Descriptions of the observations can be obtained on the STScI website via the Cycle 7 proposal number or PI name (ERO 7120: Skinner; ERO 7115: Hines). Overall, the NICMOS and ground-based polarimetry agree remarkably well, once the NICMOS polarimetric images have been binned to match the spatial resolution of the ground-based images.

NIC1 - IRC +10216

  

Figure: (after HSL) J-Band Imaging Polarimetry of IRC +10216 observed from the ground (Kastner & Weintraub 1994), compared with data obtained using NICMOS Camera 1 and reduced with the HSL and ``standard theory'' algorithms. The data reduced with the HSL algorithm agree well with the ground based data. For clarity, the NICMOS polarization vectors are plotted for $5 \times 5$ pixel bins, and the faintest and brightest intensity contours have been omitted.

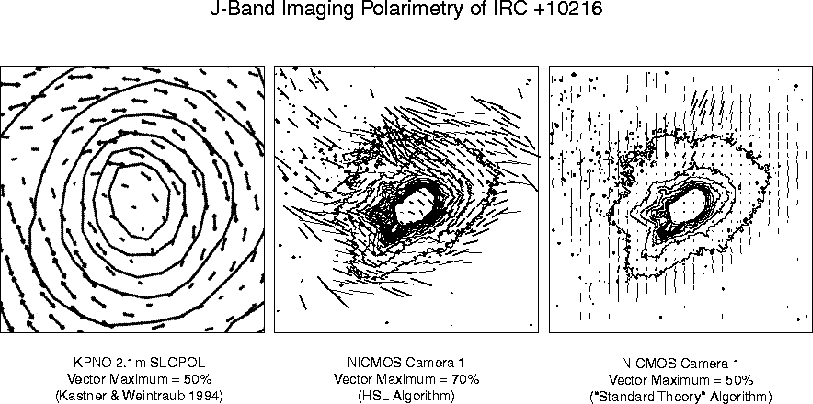Figure 1 presents the NICMOS polarimetry results for IRC +10216 (Skinner et al. 1997) compared with the ground-based data from Kastner & Weintraub (1994). The polarization map derived by processing the NICMOS data with the new HSL algorithm (center panel) agrees well with the ground based data. In contrast, polarization images derived by using the ``standard theory'' underestimate the polarization and lead to incorrectly oriented electric vector position angles. Variations of the percentage polarization in relatively uniform regions of the HSL-reduced IRC +10216 data suggest uncertainties $\sigma_{p,{\rm meas}} \mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}1-3\%$ (in percentage polarization per pixel), and comparison with the ground-based data suggests an uncertainty in the position angles $\sim 2\deg$ in a $5 \times 5$ pixel bins (Fig. 1).

NIC2 - CRL 2688

  

Figure: (after HSL) 2$\mu$m Imaging Polarimetry of CRL 2688 (The Egg Nebula) using NICMOS Camera 2, and the Cryogenic Optical Bench (COB) attached to the 2.1m at Kitt Peak (courtesy of J. Kastner). For clarity, the vectors in the NICMOS and COB data are binned by $5 \times 5$ and $4\times 4$ pixels respectively.

Figure 2 presents the NICMOS polarimetry results for CRL 2688 compared with observations obtained from the ground (Sahai et al. 1998). In this case the ground-based data are of exceptional quality and allow a more detailed comparison than for IRC +10216. Overall, the NICMOS and ground-based data agree quite well and show centrosymmetric patterns of position angle within the polar lobes.

Other, more subtle, features of the polarization morphology that are seen in the ground-based polarization map are reproduced precisely in the NICMOS map, confirming that the NICMOS polarimetry is well calibrated. However, the superior resolution of the NICMOS data reveals polarization features that are not apparent in the ground-based polarization map. In particular we note the very high polarizations ( $\sim 70-80\%$) in the arcs and filamentary structures -- features that are washed out (beam averaged) in the ground-based images resulting in lower observed polarization. As for IRC +10216, uncertainties in the spacecraft data are estimated to be $\sim 1-3\%$ in percentage polarization, and $\sim 2\deg$ in the position angles.

NICMOS Imaging Polarimetry

As illustrated by the calibration data and EROs discussed above, the NICMOS system is capable of producing accurate imaging polarimetry. The refined coefficients of the HSL algorithm enable investigation of polarization to lower limits than had originally been estimated by HSL.

Limiting Polarization: Because the errors for percentage polarization follow a Rice distribution, precise polarimetry requires measurements such that $p/\sigma_{p,{\rm meas}} > 4$ (Simmons & Stewart 1985). Therefore, uncertainties $\sigma_{p,{\rm meas}} \approx$ 0.5-3% (per pixel) imply that objects should have minimum polarizations of at least 2-12% per pixel. Binning the Stokes parameters before forming the percentage polarization (p) and the position angles reduces the uncertainties by $\sim 1/\sqrt{N}$, where N is the number of pixels in the bin. Uncertainties as low as $0.2\%$ should be achievable with bright objects.

Limiting Brightness of the Target: In a perfect photon-counting system, $\sigma_{p,{\rm phot}}$ $\approx \sqrt{2/E}$, where E is the total number of photons counted. For CRL 2688, the signal strength even in regions of low intensity (e.g. the H₂-emitting torus) should have produced $\sigma_{p,{\rm phot}}$ $\mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}$ 1%. We measure $\sigma_{p, {\rm meas}}$ $\approx 1-3\%$, which suggests the presence of other noise sources (e.g. flat-field errors).

  

Figure 3: (after HSL) Fractional signal measured in each NICMOS polarizer as a function of incident electric vector position angle (PA) for 20% polarized light. The lower curves are the differences in fractional signal between images taken with successive polarizers. The vertical dashed lines in the left panel (NIC1) represent the position angles of the incoming electric vector where these differences are all small, and thus produce the largest uncertainties in the polarization.

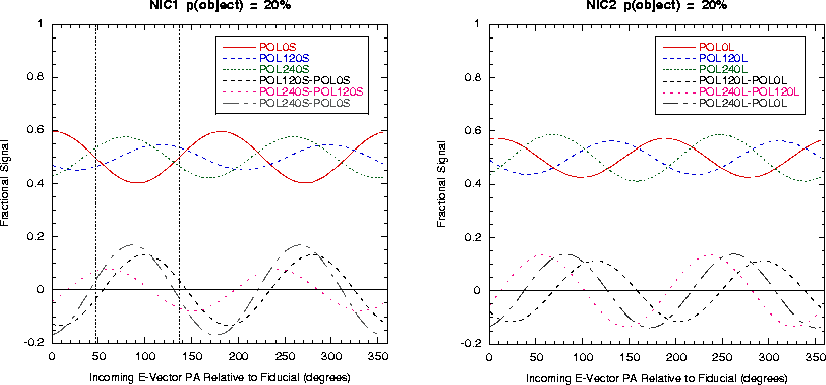Position Angle of Incoming Polarization Relative to NICMOS Orientation: The non-optimum polarizer orientations and efficiencies cause the uncertainty in polarization to be a function of the position angle of the electric vector of the incoming light. For observations with low signal-to-noise ratios (per polarizer image), and targets with lower polarizations, the difference between the signals in the images from the three polarizers becomes dominated by (photon) noise rather than analyzed polarization signal. Therefore, observations that place important incoming electric vectors at $\approx$ 45 and $\approx$ 135 in the NICMOS aperture reference frame should be avoided in NIC1. No such restriction is necessary for NIC2.

Future Directions

Further analysis of the Cycle 7 calibration data, and comparisons between NICMOS and ground-based observations of GTO and GO targets should allow even more improvements in the HSL coefficients. A detailed error analysis of the HSL algorithm is also in progress.

We have demonstrated that NICMOS can produce highly accurate images in polarized light despite its non-ideal polarimetry optics. The HSL algorithm may be useful in processing data from other instruments that use polarimetry designs like NICMOS, such as the Faint Object Camera and the Advanced Camera for Surveys.

It is a pleasure to thank B. Stobie, L. Bergeron and A. Evans for assistance with the (non-polarimetric) data calibration. Special thanks to Joel Kastner for the use of his COB observations of CRL 2688 in advance of publication, and to the late Chris Skinner for his initial processing of the IRC +10216 data. DCH acknowledges support from the NICMOS project under NASA grant NAG 5-3042.